TQC 2024: 9-13 September 2024 in Okinawa, Japan
The Theory of Quantum Computation, Communication and Cryptography (TQC) is a leading annual international conference for students and researchers working in the theoretical aspects of quantum information science. The scientific objective is to bring together the theoretical quantum information science community to present and discuss the latest advances in the field.
The 19th TQC was hosted by OIST in Okinawa, Japan, in September 2024. It was a hybrid event, with focus on in-person participation. Talks were streamed live.
Watch the livestreams on YouTube
The lists of 92 accepted talks and 429 accepted posters are now available.
Invited speakers
Potential and Limitations of Near-Term Quantum Computing
Quantum computers promise the efficient solution of some highly structured computational problems that are classically intractable. While for many years they have been primarily objects of theoretical study, only recently have efforts to build intermediate-scale quantum computers taken off. This creates an interesting state of affairs, but at the same time, it begs the question of what such devices are, practically speaking, good for. In this talk, we will present some encouraging as well as—emphasizing the latter—discouraging insights into near-term quantum computing. We will discuss rigorous quantum advantages in paradigmatic problems [1,2] and explore the use of quantum computers in machine learning [3,4] and optimization [5]. The second part of the talk will focus on the significant limitations that arise. We will emphasize identifying limitations to quantum error mitigation for shallow quantum circuits in the worst case [6]. Interestingly, it may depend on the nuances of non-unital quantum noise to what extent quantum computing without error correction may be feasible [7]. We will also provide efficient classical algorithms for instances of quantum algorithms, hence "de-quantizing" them [7-9]. The talk will conclude with the note that quantum simulation remains, to date, one of the most promising applications of near-term quantum devices [10,11].
[1] Rev. Mod. Phys. 95, 035001 (2023).
[2] arXiv:2307.14424, Nature Comm. (2024).
[3] Nature Comm. 15, 434 (2024).
[4] Nature Comm. 15, 2277 (2024).
[5] Science Adv. 10, eadj5170 (2024).
[6] arXiv:2210.11505, Nature Phys. (2024).
[7] arXiv:2403.13927 (2024).
[8] arXiv:2309.11647 (2023).
[9] Phys. Rev. Lett. 131, 100803 (2023).
[10] Nature Comm. 14, 3895 (2023).
[11] arXiv:2108.08319, Nature Comm. (2024).
Forward and Backward Mappings for Quantum Graphical Models
Graphical models offer a unifying framework for various statistical learning algorithms and models. Central to these models are the forward and backward mapping problems, which have been studied through both exact and approximate algorithms. This talk explores these mapping problems within the context of quantum graphical models, where quantum states generalize classical probability distributions.
The forward mapping problem involves deriving mean parameters from model parameters and is closely linked to approximating the partition function---a typically challenging task often requiring heuristics and approximations. We'll discuss quantum belief propagation, which has shown success in one-dimensional systems, as well as variational methods such as Markov entropy decomposition that tackle the problem from an optimization perspective.
The task of the backward mapping problem aims to compute model parameters from mean parameters. It is related to the Hamiltonian learning problem, a topic of growing interest in quantum information science lately. We'll review some existing algorithms and introduce the quantum iterative scaling (QIS) algorithm that reduces the backward mapping problem to a series of forward mapping problems. We'll present a convergence proof for QIS and demonstrate its advantages over gradient descent methods. Furthermore, we'll explore how quasi-Newton methods can enhance QIS and gradient descent algorithms, showcasing significant efficiency improvements.
Understanding Cryptographic Hardness in a Quantum World
A flurry of exciting, recent work has shown that the mathematical hardness required to realize cryptosystems such as bit commitments and secure computation in a quantum world can be significantly weaker than the hardness required for classical cryptography. This talk will discuss recent progress and some remaining challenges in understanding the assumptions that enable cryptography in a quantum world.
Quantum cryptography without one-way functions
The existence of one-way functions is the minimum assumption in classical cryptography. On the other hand, in quantum cryptography where quantum computing and quantum communications are possible, recent studies have demonstrated that the existence of one-way functions is not necessarily the minimum assumption.
Several new fundamental primitives have been introduced, such as pseudorandom unitaries, pseudorandom states, one-way state generators, EFI pairs, and one-way puzzles. They seem to be weaker than one-way functions, but still imply many useful applications, such as secret-key encryption, message authentication codes, digital signatures, private-key quantum money, commitments, and multiparty computations, etc. In this talk, I explain the basics of this “quantum cryptography without one-way functions” and give many open problems that I want to know the answers to.
Sponsors and organization of TQC 2023
Platinum sponsors
The Quantum Computing team at JPMorganChase's Global Technology Applied Research Center is at the forefront of advancing both the theoretical and practical aspects of quantum and quantum-inspired algorithms. They are currently seeking talented individuals for summer internships, as well as full-time positions for research scientists and software engineers at all experience levels. Join the firm in pushing the boundaries of quantum computing technology. Apply for open positions here.
Gold sponsors
We are hiring! Check out quantum career opportunities at Google.
Horizon Quantum Computing is developing a new generation of programming tools to simplify and expedite the process of developing software for quantum computers. By removing the need for prior quantum computing experience to develop applications for quantum hardware, Horizon’s tools are making the power of quantum computing accessible to every software developer.
We are hiring! Check out quantum career opportunities at Horizon: https://www.horizonquantum.com/careers
Silver Sponsors
Quantinuum's mission is to accelerate quantum computing and use its power to positively transform the world. By applying the laws of quantum physics to computing, we will achieve unprecedented breakthroughs in drug discovery, healthcare, materials science, cybersecurity, energy transformation, and climate change.
People and Committees of TQC 2024
Steering Committee of TQC 2024
- Andris Ambainis, University of Latvia
- Eric Chitambar, University of Illinois at Urbana-Champaign
- Kai-Min Chung, Academia Sinica
- Steve Flammia, AWS Center for Quantum Computing
- François Le Gall, Nagoya University [co-chair]
- Min-Hsiu Hsieh, Hon Hai (Foxconn) [chair]
- Kae Nemoto, OIST
- Lídia del Rio, Squids and University of Zurich
Programme Committee of TQC 2024
- Frédéric Mangiez, CNRS [chair]
- Alex Bredariol Grilo, CNRS [co-chair]
- Srinivasan Arunachalam, IBM
- Alexander Belovs, University of Latvia
- Mario Berta, RWTH Aachen University
- Xavier Bonnetain, Inria Nancy
- Jop Briet, CWI
- Marco Cerezo, LANL
- Nai-Hui Chia, Rice University
- Nicolas Delfosse, IonQ
- Ernesto Galvão, INL
- Uma Girish, Princeton
- Tom Gur, University of Cambridge
- Yassine Hamoudi, CNRS Bordeaux
- Dominik Hangleiter, QuICS (UMD & NIST)
- Chris Heunen, University of Edinburgh
- Christoph Hirche, TU Munich and CQT NUS
- Nick Hunter-Jones, UT Austin
- John Kallaugher, Sandia National Laboratories
- Shelby Kimmel, Middlebury College
- Robert Koenig, TU Munich
- Felix Leditzky, UIUC
- Tongyang Li , Peking University
- Jiahui Liu, MIT
- Alex May, Perimeter Institute and University of Waterloo
- Mio Murao, University of Tokyo
- Ion Nechita, CNRS, Toulouse
- Harumichi Nishimura, Nagoya University
- Tom O’Brien, Google Quantum AI
- Subhasree Patro, Utrecht University and QuSoft
- Supartha Podder, Stony Brook University
- Alexander Poremba, MIT
- Luowen Qian, Boston University
- Patrick Rebentrost, CQT
- Norbert Schuch, University of Vienna
- Thomas Schuster, Caltech
- Makrand Sinha, UIUC
- Fang Song, Portland State University
- David Sutter, IBM Zurich
- Mario Szegedy, Rutgers University
- Marcelo Terra Cunha, Unicamp
- Dave Touchette, Sherbrooke University
- Dominic Verdon, University of Bristol
- Nathan Wiebe, University of Toronto
- Dominic Williamson, University of Sydney
- Penghui Yao, Nanjing University
- Ted Yoder, IBM
Organising Committee of TQC 2024
Local organizers in Okinawa:
- David Elkouss Coronas, OIST
- Kae Nemoto, OIST
- Slawomir Rosiek, OIST
- Yukari Yoseda, OIST
International organizers:
- Lídia del Rio, Squids and University of Zurich
- Nuriya Nurgalieva, Squids and University of Zurich
Search accepted talks and posters for TQC 2024
The full lists of accepted talks and accepted posters are now published!
Libor Caha, Xavier Coiteux-Roy, Robert Koenig
A colossal advantage: 3D-local noisy shallow quantum circuits defeat unbounded fan-in classical circuits Talk
2024.
Abstract | Tags: Tuesday | Links:
@Talk{T24_208,
title = {A colossal advantage: 3D-local noisy shallow quantum circuits defeat unbounded fan-in classical circuits},
author = {Libor Caha and Xavier Coiteux-Roy and Robert Koenig},
url = {https://arxiv.org/abs/2312.09209},
year = {2024},
date = {2024-01-01},
abstract = {We present a computational problem with the following properties: (i) Every instance can be solved with near-certainty by a constant-depth quantum circuit using only nearest-neighbor gates in 3D even when its implementation is corrupted by noise. (ii) Any constant-depth classical circuit composed of unbounded fan-in AND, OR, as well as NOT gates, i.e., an AC0-circuit, of size smaller than a certain subexponential, fails to solve a uniformly random instance with probability greater than a certain constant. Such an advantage against unbounded fan-in classical circuits was previously only known in the noise-free case or without locality constraints. We overcome these limitations, proposing a quantum advantage demonstration amenable to experimental realizations. Subexponential circuit-complexity lower bounds have traditionally been referred to as exponential. We use the term colossal since our fault-tolerant 3D architecture resembles a certain Roman monument.},
keywords = {Tuesday},
pubstate = {published},
tppubtype = {Talk}
}
David Cui, Giulio Malavolta, Arthur Mehta, Anand Natarajan, Connor Paddock, Simon Schmidt, Michael Walter, Tina Zhang
A Computational Tsirelson's Theorem for the Value of Compiled XOR Games Talk
2024.
Abstract | Tags: Tuesday | Links:
@Talk{T24_235,
title = {A Computational Tsirelson's Theorem for the Value of Compiled XOR Games},
author = {David Cui and Giulio Malavolta and Arthur Mehta and Anand Natarajan and Connor Paddock and Simon Schmidt and Michael Walter and Tina Zhang},
url = {https://arxiv.org/abs/2402.17301},
year = {2024},
date = {2024-01-01},
abstract = {Nonlocal games are a foundational tool for understanding entanglement and constructing quantum protocols in settings with multiple spatially separated quantum devices. In this work, we continue the study initiated by Kalai et al. (STOC '23) of compiled nonlocal games, played between a classical verifier and a single cryptographically limited quantum device. Our main result is that the compiler proposed by Kalai et al. is sound for any two-player XOR game. A celebrated theorem of Tsirelson shows that for XOR games, the quantum value is exactly given by a semidefinite program, and we obtain our result by showing that the SDP upper bound holds for the compiled game up to a negligible error arising from the compilation. This answers a question raised by Natarajan and Zhang (FOCS '23), who showed soundness for the specific case of the CHSH game. Using our techniques, we obtain several additional results, including (1) tight bounds on the compiled value of parallel-repeated XOR games, (2) operator self-testing statements for any compiled XOR game, and (3) a ``nice" sum-of-squares certificate for any XOR game, from which operator rigidity is manifest.},
keywords = {Tuesday},
pubstate = {published},
tppubtype = {Talk}
}
Alexander Dalzell
A shortcut to a near-optimal quantum linear system solver Talk
2024.
@Talk{T24_325,
title = {A shortcut to a near-optimal quantum linear system solver},
author = {Alexander Dalzell},
year = {2024},
date = {2024-01-01},
abstract = {Given a linear system of equations Ax = b, quantum linear system solvers (QLSSs) approximately prepare a quantum state |x⟩ for which the amplitudes are proportional to the solution vector x. Asymptotically optimal QLSSs have query complexity O(κlog(1/ε)), where κ is the condition number of A, and ε is the approximation error. However, runtime guarantees for existing optimal and near-optimal QLSSs do not have favorable constant factors, in part because they rely on complex or difficult-to-analyze techniques like variable-time amplitude amplification and adiabatic path-following. Here, we give a conceptually simple, near-optimal QLSS that does not use these techniques. If the solution norm ∥x∥∥A∥/∥b∥ is known exactly, our QLSS requires only a single application of kernel reflection (an extension of eigenstate filtering), and has query complexity (1 + O(ε))κ ln(2√2/ε). If the norm is not known, it can be estimated up to a constant factor using O(log log(κ)) applications of kernel projection (a slight generalization of eigenstate filtering), yielding a QLSS with near-optimal total complexity O(κ log log(κ) log log log(κ) + κ log(1/ε)). Preliminary constant-factor analysis suggests that for practical values of κ, ε our QLSS provides rigorous guarantees that are at least an order of magnitude better than previous guarantees.},
keywords = {Tuesday},
pubstate = {published},
tppubtype = {Talk}
}
Yijia Xu, Yixu Wang, Victor V. Albert
Clifford operations and homological codes for rotors and oscillators Talk
2024.
Abstract | Tags: Tuesday | Links:
@Talk{T24_299,
title = {Clifford operations and homological codes for rotors and oscillators},
author = {Yijia Xu and Yixu Wang and Victor V. Albert},
url = {https://arxiv.org/abs/2311.07679},
year = {2024},
date = {2024-01-01},
abstract = {We develop quantum information processing primitives for the planar rotor, the state space of a particle on a circle. The n-rotor Clifford group, U(1)n(n+1)/2 ⋊ GLn(Z), is represented by continuous U(1) gates generated by polynomials quadratic in angular momenta, as well as discrete GLn(Z) gates generated by momentum sign-flip and sum gates. Understandings in rotor
Clifford group allow us to establish connections between homological rotor error-correcting codes and oscillator quantum codes, including Gottesman-Kitaev-Preskill codes and rotation-symmetric bosonic codes. Inspired by homological rotor codes, we provide a systematic construction of multi-mode rotation-symmetric bosonic codes by analoging Fock states to rotor states with non-negative angular momentum. This new family of multi-mode bosonic codes protect against dephasing and changes in occupation numbers, which we call homological number-phase codes. Their encoding and decoding circuits are readily derived from the corresponding
rotor Clifford operations. In particular, we show how to non-destructively measure the oscillator phase using conditional occupation-number addition and post-selection. We also outline several
rotor and oscillator varieties of the GKP-stabilizer codes.
References: arXiv:2311.07679, homological rotor error-correcting codes
(arXiv:2303.13723), GKP-stabilizer codes (arXiv:1903.12615)},
keywords = {Tuesday},
pubstate = {published},
tppubtype = {Talk}
}
Clifford group allow us to establish connections between homological rotor error-correcting codes and oscillator quantum codes, including Gottesman-Kitaev-Preskill codes and rotation-symmetric bosonic codes. Inspired by homological rotor codes, we provide a systematic construction of multi-mode rotation-symmetric bosonic codes by analoging Fock states to rotor states with non-negative angular momentum. This new family of multi-mode bosonic codes protect against dephasing and changes in occupation numbers, which we call homological number-phase codes. Their encoding and decoding circuits are readily derived from the corresponding
rotor Clifford operations. In particular, we show how to non-destructively measure the oscillator phase using conditional occupation-number addition and post-selection. We also outline several
rotor and oscillator varieties of the GKP-stabilizer codes.
References: arXiv:2311.07679, homological rotor error-correcting codes
(arXiv:2303.13723), GKP-stabilizer codes (arXiv:1903.12615)
Andreas Bauer
Fault-tolerant circuits from twisted quantum doubles – Quantum error correction beyond stabilizer and Clifford Talk
2024.
Abstract | Tags: Tuesday | Links:
@Talk{T24_407,
title = {Fault-tolerant circuits from twisted quantum doubles – Quantum error correction beyond stabilizer and Clifford},
author = {Andreas Bauer},
url = {https://arxiv.org/pdf/2403.12119},
year = {2024},
date = {2024-01-01},
abstract = {We propose a family of explicit geometrically local circuits realizing any abelian non-chiral topological phase as an actively error-corrected fault-tolerant memory.
These circuits are constructed from measuring 1-form symmetries in discrete fixed-point path integrals, which we express through cellular cohomology and higher-order cup products.
The specific path integral we use is the abelian Dijkgraaf-Witten state sum on a 3-dimensional cellulation, which is a spacetime representation of the twisted quantum double model.
The resulting circuits are based on a syndrome extraction circuit of the (qudit) stabilizer toric code, into which we insert non-Clifford phase gates that implement the ``twist''.
The overhead compared to the toric code is moderate, in contrast to known constructions for twisted abelian phases.
The simplest non-trivial example is a fault-tolerant circuit for the double-semion phase, defined on the same set of qubits as the stabilizer toric code, with $12$ controlled-$S$ gates in addition to the $8$ controlled-$X$ gates and $2$ single-qubit measurements of the toric code per spacetime unit cell.
We also show that other architectures for the (qudit) toric code phase, like measurement-based topological quantum computation or Floquet codes, can be enriched with phase gates to implement twisted quantum doubles instead of their untwisted versions.
As a further result, we prove fault tolerance under arbitrary local (including non-Pauli) noise for a very general class of topological circuits that we call 1-form symmetric fixed-point circuits.
This notion unifies the circuits in this paper as well as the stabilizer toric code, subsystem toric code, measurement-based topological quantum computation, or the (CSS) honeycomb Floquet code. We also demonstrate how our method can be adapted to construct fault-tolerant circuits for specific non-Abelian phases.},
keywords = {Tuesday},
pubstate = {published},
tppubtype = {Talk}
}
These circuits are constructed from measuring 1-form symmetries in discrete fixed-point path integrals, which we express through cellular cohomology and higher-order cup products.
The specific path integral we use is the abelian Dijkgraaf-Witten state sum on a 3-dimensional cellulation, which is a spacetime representation of the twisted quantum double model.
The resulting circuits are based on a syndrome extraction circuit of the (qudit) stabilizer toric code, into which we insert non-Clifford phase gates that implement the ``twist''.
The overhead compared to the toric code is moderate, in contrast to known constructions for twisted abelian phases.
The simplest non-trivial example is a fault-tolerant circuit for the double-semion phase, defined on the same set of qubits as the stabilizer toric code, with $12$ controlled-$S$ gates in addition to the $8$ controlled-$X$ gates and $2$ single-qubit measurements of the toric code per spacetime unit cell.
We also show that other architectures for the (qudit) toric code phase, like measurement-based topological quantum computation or Floquet codes, can be enriched with phase gates to implement twisted quantum doubles instead of their untwisted versions.
As a further result, we prove fault tolerance under arbitrary local (including non-Pauli) noise for a very general class of topological circuits that we call 1-form symmetric fixed-point circuits.
This notion unifies the circuits in this paper as well as the stabilizer toric code, subsystem toric code, measurement-based topological quantum computation, or the (CSS) honeycomb Floquet code. We also demonstrate how our method can be adapted to construct fault-tolerant circuits for specific non-Abelian phases.
Robbie King, Tamara Kohler
Gapped Clique Homology is QMA1-hard and contained in QMA Talk
2024.
@Talk{T24_10,
title = {Gapped Clique Homology is QMA1-hard and contained in QMA},
author = {Robbie King and Tamara Kohler},
year = {2024},
date = {2024-01-01},
abstract = {We study the complexity of a classic problem in computational topology, the homology problem: given a description of some space X and an integer k, decide if X contains a k-dimensional hole. The setting and statement of the homology problem are completely classical, yet we find that the complexity is characterized by quantum complexity classes. Our result can be seen as an aspect of a connection between homology and supersymmetric quantum mechanics [Wit82]. We consider clique complexes, motivated by the practical application of topological data analysis (TDA). The clique complex of a graph is the simplicial complex formed by declaring every k+1-clique in the graph to be a k-simplex. Our main result is that deciding whether the clique complex of a weighted graph has a hole or not, given a suitable promise on the gap, is QMA1-hard and contained in QMA. Our main innovation is a technique to lower bound the eigenvalues of the combinatorial Laplacian operator. For this, we invoke a tool from algebraic topology known as spectral sequences. In particular, we exploit a connection between spectral sequences and Hodge theory [For94]. Spectral sequences will play a role analogous to perturbation theory for combinatorial Laplacians. In addition, we develop the simplicial surgery technique used in prior work [CK22]. Our result provides some suggestion that the quantum TDA algorithm [LGZ16] cannot be dequantized. More broadly, we hope that our results will open up new possibilities for quantum advantage in topological data analysis.},
keywords = {Tuesday},
pubstate = {published},
tppubtype = {Talk}
}
Sergey Bravyi, Natalie Parham, Minh Tran
Identity check problem for shallow quantum circuits Talk
2024.
Abstract | Tags: Tuesday | Links:
@Talk{T24_233,
title = {Identity check problem for shallow quantum circuits},
author = {Sergey Bravyi and Natalie Parham and Minh Tran},
url = {https://arxiv.org/pdf/2401.16525},
year = {2024},
date = {2024-01-01},
abstract = {Checking whether two quantum circuits are approximately equivalent is a common task in quantum computing. We consider a closely related identity check problem: given a quantum circuit U, one has to estimate the diamond-norm distance between U and the identity channel. We present a classical algorithm approximating the distance to the identity within a factor alpha = D+1 for shallow geometrically local D-dimensional circuits provided that the circuit is sufficiently close to the identity. The runtime of the algorithm scales linearly with the number of qubits for any constant circuit depth and spatial dimension. We also show that the operator-norm distance to the identity || U - I || can be efficiently approximated within a factor alpha = 5 for shallow 1D circuits and, under a certain technical condition, within a factor alpha = 2D + 3 for shallow D-dimensional circuits. A numerical implementation of the identity check algorithm is reported for 1D Trotter circuits with up to 100 qubits.},
keywords = {Tuesday},
pubstate = {published},
tppubtype = {Talk}
}
Zhili Chen, Joshua A. Grochow, Youming Qiao, Gang Tang, Chuanqi Zhang
Multipartite to tripartite reductions for LU and SLOCC equivalences Talk
2024.
Tags: Tuesday | Links:
@Talk{T24_23,
title = {Multipartite to tripartite reductions for LU and SLOCC equivalences},
author = {Zhili Chen and Joshua A. Grochow and Youming Qiao and Gang Tang and Chuanqi Zhang},
url = {https://arxiv.org/abs/2306.03135 https://arxiv.org/abs/1907.00309},
year = {2024},
date = {2024-01-01},
keywords = {Tuesday},
pubstate = {published},
tppubtype = {Talk}
}
Antonio Anna Mele, Armando Angrisani, Soumik Ghosh, Sumeet Khatri, Jens Eisert, Daniel Stilck Franca, Yihui Quek
Noise-induced shallow circuits and absence of barren plateaus Talk
2024.
Abstract | Tags: Tuesday | Links:
@Talk{T24_409,
title = {Noise-induced shallow circuits and absence of barren plateaus},
author = {Antonio Anna Mele and Armando Angrisani and Soumik Ghosh and Sumeet Khatri and Jens Eisert and Daniel Stilck Franca and Yihui Quek},
url = {https://arxiv.org/abs/2403.13927},
year = {2024},
date = {2024-01-01},
abstract = {Motivated by realistic hardware considerations of the pre-fault-tolerant era, we comprehensively study the impact of uncorrected noise on quantum circuits. We first show that any noise `truncates' most quantum circuits to effectively logarithmic depth, in the task of computing Pauli expectation values. We then prove that quantum circuits under any non-unital noise exhibit lack of barren plateaus for cost functions composed of local observables. But, by leveraging the effective shallowness, we also design a classical algorithm to estimate Pauli expectation values within inverse-polynomial additive error with high probability over the ensemble. Its runtime is independent of circuit depth and it operates in polynomial time in the number of qubits for one-dimensional architectures and quasi-polynomial time for higher-dimensional ones. Taken together, our results showcase that, unless we carefully engineer the circuits to take advantage of the noise, it is unlikely that noisy quantum circuits are preferable over shallow quantum circuits for algorithms that output Pauli expectation value estimates, like many variational quantum machine learning proposals. Moreover, we anticipate that our work could provide valuable insights into the fundamental open question about the complexity of sampling from (possibly non-unital) noisy random circuits.},
keywords = {Tuesday},
pubstate = {published},
tppubtype = {Talk}
}
Atsuya Hasegawa, Srijita Kundu, Harumichi Nishimura
On the Power of Quantum Distributed Proofs Talk
2024.
Abstract | Tags: Tuesday | Links:
@Talk{T24_132,
title = {On the Power of Quantum Distributed Proofs},
author = {Atsuya Hasegawa and Srijita Kundu and Harumichi Nishimura},
url = {https://arxiv.org/abs/2403.14108},
year = {2024},
date = {2024-01-01},
abstract = {Quantum nondeterministic distributed computing was recently introduced as dQMA (distributed quantum Merlin-Arthur) protocols by Fraigniaud, Le Gall, Nishimura and Paz (ITCS 2021). In dQMA protocols, with the help of quantum proofs and local communication, nodes on a network verify a global property of the network. Fraigniaud et al. showed that, when the network size is small, there exists an exponential separation in proof size between distributed classical and quantum verification protocols, for the equality problem, where the verifiers check if all the data owned by a subset of them are identical. In this paper, we further investigate and characterize the power of the dQMA protocols for various decision problems.
First, we give a more efficient dQMA protocol for the equality problem with a simpler analysis. This is done by adding a symmetrization step on each node and exploiting properties of the permutation test, which is a generalization of the SWAP test. We also show a quantum advantage for the equality problem on path networks still persists even when the network size is large, by considering ``relay points'' between extreme nodes.
Second, we show that even in a general network, there exist efficient dQMA protocols for the ranking verification problem, the Hamming distance problem, and more problems that derive from efficient quantum one-way communication protocols. Third, in a line network, we construct an efficient dQMA protocol for a problem that has an efficient two-party QMA communication protocol. Finally, we obtain the first lower bounds on the proof and communication cost of dQMA protocols. To prove a lower bound on the equality problem, we show any dQMA protocol with an entangled proof between nodes can be simulated with a dQMA protocol with a separable proof between nodes by using a QMA communication-complete problem introduced by Raz and Shpilka (CCC 2004).},
keywords = {Tuesday},
pubstate = {published},
tppubtype = {Talk}
}
First, we give a more efficient dQMA protocol for the equality problem with a simpler analysis. This is done by adding a symmetrization step on each node and exploiting properties of the permutation test, which is a generalization of the SWAP test. We also show a quantum advantage for the equality problem on path networks still persists even when the network size is large, by considering ``relay points'' between extreme nodes.
Second, we show that even in a general network, there exist efficient dQMA protocols for the ranking verification problem, the Hamming distance problem, and more problems that derive from efficient quantum one-way communication protocols. Third, in a line network, we construct an efficient dQMA protocol for a problem that has an efficient two-party QMA communication protocol. Finally, we obtain the first lower bounds on the proof and communication cost of dQMA protocols. To prove a lower bound on the equality problem, we show any dQMA protocol with an entangled proof between nodes can be simulated with a dQMA protocol with a separable proof between nodes by using a QMA communication-complete problem introduced by Raz and Shpilka (CCC 2004).
Srinivasan Arunachalam, Vojtech Havlicek, Louis Schatzki
On the Role of Entanglement and Statistics in Learning Talk
2024.
Abstract | Tags: Tuesday | Links:
@Talk{T24_251,
title = {On the Role of Entanglement and Statistics in Learning},
author = {Srinivasan Arunachalam and Vojtech Havlicek and Louis Schatzki},
url = {https://arxiv.org/abs/2306.03161},
year = {2024},
date = {2024-01-01},
abstract = {We make progress in understanding the relationship between learning models with access to entangled, separable and statistical measurements in the quantum statistical query (QSQ) model. We show the following results.
Entangled versus separable measurements:
The goal is to learn an unknown f from the concept class C containing functions from 0,1^n to [k] given copies of a uniform superposition over |x,f(x)>. We show that, if T copies suffice to learn f using entangled measurements, O(nT^2) copies suffice to learn f using only separable measurements.
Entangled versus statistical measurements:
The goal is to learn a function f in C given access to separable measurements or statistical measurements. We exhibit a concept class C based of degree-2 functions with exponential separation between QSQ learning and quantum learning with entangled measurements (even in the presence of noise). This proves the ""quantum analogue"" of the seminal result of Blum et al. that separates classical SQ learning from classical PAC learning with classification noise.
QSQ lower bounds for learning states:
We introduce a quantum statistical query dimension (QSD), and use it to give lower bounds on the QSQ complexity of learning. We prove superpolynomial QSQ lower bounds for testing purity of quantum states, shadow tomography, learning coset states for the Abelian hidden subgroup problem, degree-2 functions, planted biclique states, and learning output states of Clifford circuits of depth polylog(n). We also show that an extension of QSD characterizes the complexity of general search problems.
Further applications: We give an unconditional separation between weak and strong error mitigation and prove lower bounds for learning distributions in the QSQ model. Prior works by Quek et al., Hinsche et al., and Nietner et al. proved analogous results assuming diagonal measurements and our work removes this assumption.},
keywords = {Tuesday},
pubstate = {published},
tppubtype = {Talk}
}
Entangled versus separable measurements:
The goal is to learn an unknown f from the concept class C containing functions from 0,1^n to [k] given copies of a uniform superposition over |x,f(x)>. We show that, if T copies suffice to learn f using entangled measurements, O(nT^2) copies suffice to learn f using only separable measurements.
Entangled versus statistical measurements:
The goal is to learn a function f in C given access to separable measurements or statistical measurements. We exhibit a concept class C based of degree-2 functions with exponential separation between QSQ learning and quantum learning with entangled measurements (even in the presence of noise). This proves the ""quantum analogue"" of the seminal result of Blum et al. that separates classical SQ learning from classical PAC learning with classification noise.
QSQ lower bounds for learning states:
We introduce a quantum statistical query dimension (QSD), and use it to give lower bounds on the QSQ complexity of learning. We prove superpolynomial QSQ lower bounds for testing purity of quantum states, shadow tomography, learning coset states for the Abelian hidden subgroup problem, degree-2 functions, planted biclique states, and learning output states of Clifford circuits of depth polylog(n). We also show that an extension of QSD characterizes the complexity of general search problems.
Further applications: We give an unconditional separation between weak and strong error mitigation and prove lower bounds for learning distributions in the QSQ model. Prior works by Quek et al., Hinsche et al., and Nietner et al. proved analogous results assuming diagonal measurements and our work removes this assumption.
Tomoyuki Morimae, Takashi Yamakawa
One-Wayness in Quantum Cryptography Talk
2024.
Abstract | Tags: Proceedings, Tuesday | Links:
@Talk{T24_12,
title = {One-Wayness in Quantum Cryptography},
author = {Tomoyuki Morimae and Takashi Yamakawa},
url = {https://arxiv.org/abs/2210.03394},
year = {2024},
date = {2024-01-01},
abstract = {The existence of one-way functions is one of the most fundamental assumptions in classical cryptography. In the quantum world, on the other hand, there are evidences that some cryptographic primitives can exist even if one-way functions do not exist. We therefore have the following important open problem in quantum cryptography: What is the most fundamental element in quantum cryptography? In this direction, Brakerski, Canetti, and Qian recently defined a notion called EFI pairs, which are pairs of efficiently generatable states that are statistically distinguishable but computationally indistinguishable, and showed its equivalence with some cryptographic primitives including commitments, oblivious transfer, and general multi-party computations. However, their work focuses on decision-type primitives and does not cover search-type primitives like quantum money and digital signatures. In this paper, we study properties of one-way state generators (OWSGs), which are a quantum analogue of one-way functions. We first revisit the definition of OWSGs and generalize it by allowing mixed output states. Then we show the following results. (1) We define a weaker version of OWSGs, weak OWSGs, and show that they are equivalent to OWSGs. (2) Quantum digital signatures are equivalent to OWSGs. (3) Private-key quantum money schemes (with pure money states) imply OWSGs. (4) Quantum pseudo one-time pad schemes imply both OWSGs and EFI pairs. (5) We introduce an incomparable variant of OWSGs, which we call secretly-verifiable and statistically-invertible OWSGs, and show that they are equivalent to EFI pairs.},
keywords = {Proceedings, Tuesday},
pubstate = {published},
tppubtype = {Talk}
}
Shalev Ben-David, Srijita Kundu
Oracle separation of QMA and QCMA with bounded adaptivity Talk
2024.
Abstract | Tags: Tuesday | Links:
@Talk{T24_249,
title = {Oracle separation of QMA and QCMA with bounded adaptivity},
author = {Shalev Ben-David and Srijita Kundu},
url = {https://arxiv.org/abs/2402.00298},
year = {2024},
date = {2024-01-01},
abstract = {We give an oracle separation between QMA and QCMA for quantum algorithms that have bounded adaptivity in their oracle queries; that is, the number of rounds of oracle calls is small, though each round may involve polynomially many queries in parallel. Our oracle construction is a simplified version of the construction used recently by Li, Liu, Pelecanos, and Yamakawa (2023), who showed an oracle separation between QMA and QCMA when the quantum algorithms are only allowed to access the oracle classically. To prove our results, we introduce a property of relations called slipperiness, which may be useful for getting a fully general classical oracle separation between QMA and QCMA.},
keywords = {Tuesday},
pubstate = {published},
tppubtype = {Talk}
}
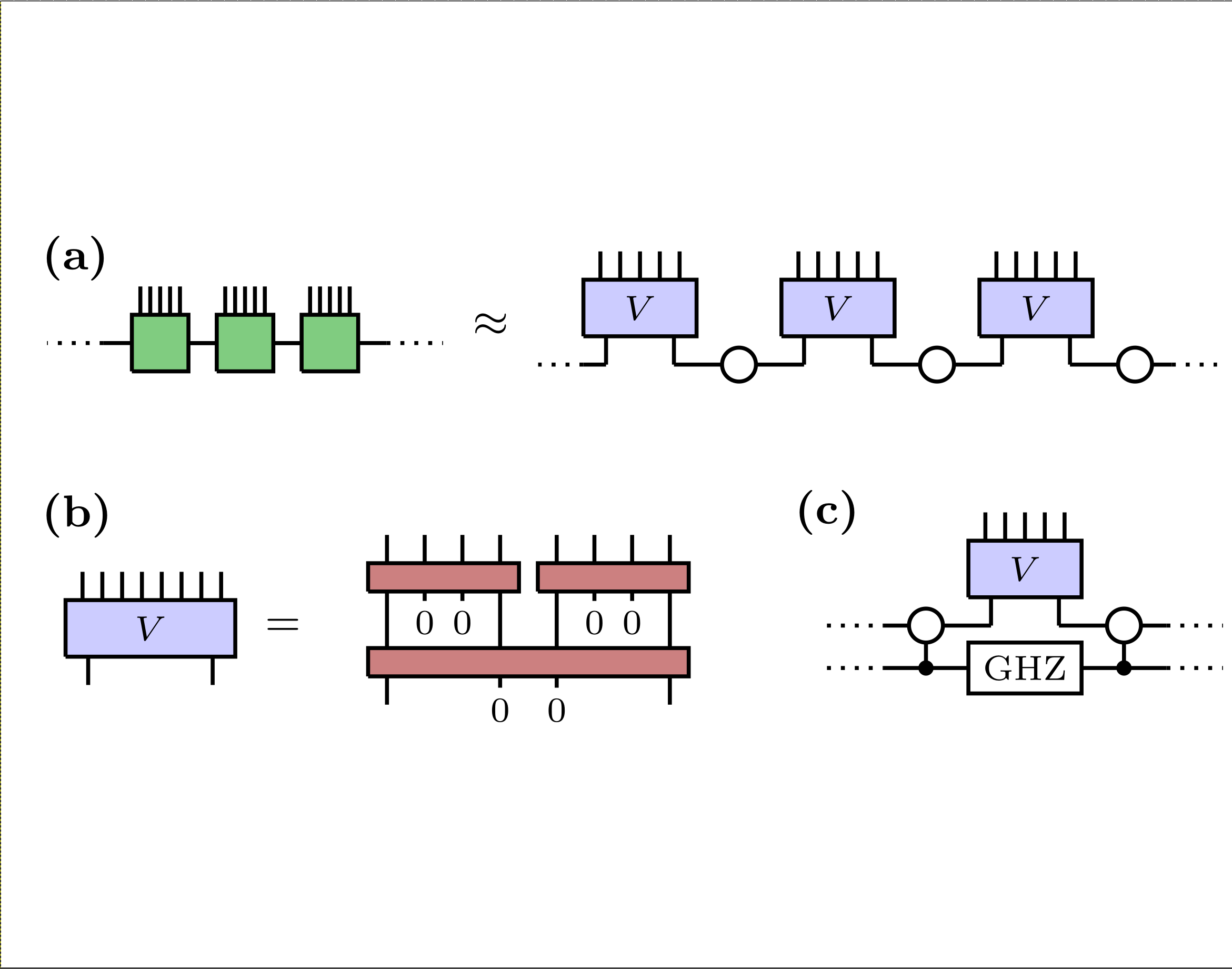
Daniel Malz, Georgios Styliaris, Zhi-Yuan Wei, J. Ignacio Cirac
Preparation of Matrix Product States with Log-Depth Quantum Circuits Talk
2024.
Abstract | Tags: Tuesday | Links:
@Talk{T24_79,
title = {Preparation of Matrix Product States with Log-Depth Quantum Circuits},
author = {Daniel Malz and Georgios Styliaris and Zhi-Yuan Wei and J. Ignacio Cirac},
url = {https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.132.040404},
year = {2024},
date = {2024-01-01},
abstract = {We consider the preparation of matrix product states (MPS) on quantum devices via quantum circuits of local gates. We first prove that faithfully preparing translation-invariant normal (i.e., short-range correlated) MPS of N sites requires a circuit depth T = Ω(log N). We then introduce an algorithm based on the renormalization-group transformation to prepare normal MPS with an error ε in depth T = O[log(N/ε)]. The algorithm has thus the fastest scaling possible for this class of states. We also show that measurement and feedback leads to an exponential speedup of the algorithm to T = O[log log(N/ε)]. Measurements also allow one to prepare arbitrary translation-invariant MPS, including long-range non-normal ones, in the same depth. Finally, the algorithm naturally extends to inhomogeneous MPS.},
keywords = {Tuesday},
pubstate = {published},
tppubtype = {Talk}
}
Sabee Grewal, Vishnu Iyer, William Kretschmer, Daniel Liang
Pseudoentanglement Ain't Cheap Talk
2024.
Abstract | Tags: Tuesday | Links:
@Talk{T24_86,
title = {Pseudoentanglement Ain't Cheap},
author = {Sabee Grewal and Vishnu Iyer and William Kretschmer and Daniel Liang},
url = {https://arxiv.org/abs/2404.00126},
year = {2024},
date = {2024-01-01},
abstract = {We show that any pseudoentangled state ensemble with a gap of t bits of entropy requires Ω(t) non-Clifford gates to prepare. This bound is tight up to polylogarithmic factors if linear-time quantum-secure pseudorandom functions exist. Our result follows from a polynomial-time algorithm to estimate the entanglement entropy of a quantum state across any cut of qubits. When run on an n-qubit state that is stabilized by at least 2^n−t Pauli operators, our algorithm produces an estimate that is within an additive factor of t/2 bits of the true entanglement entropy.},
keywords = {Tuesday},
pubstate = {published},
tppubtype = {Talk}
}
Dorian Rudolph, Sevag Gharibian, Daniel Nagaj
Quantum 2-SAT on low dimensional systems is QMA_1-complete: Direct embeddings and black-box simulation Talk
2024.
Abstract | Tags: Tuesday | Links:
@Talk{T24_73,
title = {Quantum 2-SAT on low dimensional systems is QMA_1-complete: Direct embeddings and black-box simulation},
author = {Dorian Rudolph and Sevag Gharibian and Daniel Nagaj},
url = {https://arxiv.org/abs/2401.02368},
year = {2024},
date = {2024-01-01},
abstract = {Despite the fundamental role the Quantum Satisfiability (QSAT) problem has played in quantum complexity theory, a central question remains open: At which local dimension does the complexity of QSAT transition from ""easy"" to ""hard""?
Here, we study QSAT with each constraint acting on a k-dimensional and l-dimensional qudit pair, denoted (k,l)-QSAT.
Our first main result shows that, surprisingly, QSAT on qubits can remain QMA_1-hard, in that (2,5)-QSAT is QMA_1-complete. (QMA_1 is a quantum analogue of MA with perfect completeness.)
In contrast, (2,2)-QSAT (i.e. Quantum 2-SAT on qubits) is well-known to be poly-time solvable [Bravyi, 2006]. Our second main result proves that (3,d)-QSAT on the 1D line with d = O(1) is also QMA_1-hard.
Finally, we initiate the study of (2,d)-QSAT on the 1D line by giving a frustration-free 1D Hamiltonian with a unique, entangled ground state.
As implied by our title, our first result uses a direct embedding: We combine a novel clock construction with the 2D circuit-to-Hamiltonian construction of [Gosset and Nagaj, 2013].
Of note is a new simplified and analytic proof for the latter (as opposed to a partially numeric proof in [GN13]). This exploits Unitary Labelled Graphs [Bausch, Cubitt, Ozols, 2017] together with a new ""Nullspace Connection Lemma"", allowing us to break low energy analyses into small patches of projectors, and to improve the soundness analysis of [GN13] from Omega(1/T^6) to Omega(1/T^2), for T the number of gates. Our second result goes via black-box reduction: Given an arbitrary 1D Hamiltonian H on d'-dimensional qudits, we show how to embed it into an effective 1D (3,d)-QSAT instance, for d = O(1). Our approach may be viewed as a weaker notion of ""simulation"" (à la [Bravyi, Hastings 2017], [Cubitt, Montanaro, Piddock 2018]). As far as we are aware, this gives the first ""black-box simulation""-based QMA_1-hardness result.},
keywords = {Tuesday},
pubstate = {published},
tppubtype = {Talk}
}
Here, we study QSAT with each constraint acting on a k-dimensional and l-dimensional qudit pair, denoted (k,l)-QSAT.
Our first main result shows that, surprisingly, QSAT on qubits can remain QMA_1-hard, in that (2,5)-QSAT is QMA_1-complete. (QMA_1 is a quantum analogue of MA with perfect completeness.)
In contrast, (2,2)-QSAT (i.e. Quantum 2-SAT on qubits) is well-known to be poly-time solvable [Bravyi, 2006]. Our second main result proves that (3,d)-QSAT on the 1D line with d = O(1) is also QMA_1-hard.
Finally, we initiate the study of (2,d)-QSAT on the 1D line by giving a frustration-free 1D Hamiltonian with a unique, entangled ground state.
As implied by our title, our first result uses a direct embedding: We combine a novel clock construction with the 2D circuit-to-Hamiltonian construction of [Gosset and Nagaj, 2013].
Of note is a new simplified and analytic proof for the latter (as opposed to a partially numeric proof in [GN13]). This exploits Unitary Labelled Graphs [Bausch, Cubitt, Ozols, 2017] together with a new ""Nullspace Connection Lemma"", allowing us to break low energy analyses into small patches of projectors, and to improve the soundness analysis of [GN13] from Omega(1/T^6) to Omega(1/T^2), for T the number of gates. Our second result goes via black-box reduction: Given an arbitrary 1D Hamiltonian H on d'-dimensional qudits, we show how to embed it into an effective 1D (3,d)-QSAT instance, for d = O(1). Our approach may be viewed as a weaker notion of ""simulation"" (à la [Bravyi, Hastings 2017], [Cubitt, Montanaro, Piddock 2018]). As far as we are aware, this gives the first ""black-box simulation""-based QMA_1-hardness result.
Tomoyuki Morimae, Takashi Yamakawa
Quantum Advantage from One-Way Functions Talk
2024.
Abstract | Tags: Tuesday | Links:
@Talk{T24_4,
title = {Quantum Advantage from One-Way Functions},
author = {Tomoyuki Morimae and Takashi Yamakawa},
url = {https://arxiv.org/abs/2302.04749},
year = {2024},
date = {2024-01-01},
abstract = {We demonstrate quantum advantage with several basic assumptions, specifically based on only the existence of OWFs. We introduce inefficient-verifier proofs of quantumness (IV-PoQ), and construct it from classical bit commitments. IV-PoQ is an interactive protocol between a verifier and a quantum prover consisting of two phases. In the first phase, the verifier is probabilistic polynomial-time, and it interacts with the prover. In the second phase, the verifier becomes inefficient, and makes its decision based on the transcript of the first phase. If the prover is honest, the inefficient verifier accepts with high probability, but any classical malicious prover only has a small probability of being accepted by the inefficient verifier. Our construction demonstrates the following results: (1)If one-way functions exist, then IV-PoQ exist. (2)If distributional collision-resistant hash functions exist (which exist if hard-on-average problems in SZK exist), then constant-round IV-PoQ exist. We also demonstrate quantum advantage based on worst-case-hard assumptions. We define auxiliary-input IV-PoQ (AI-IV-PoQ) that only require that for any malicious prover, there exist infinitely many auxiliary inputs under which the prover cannot cheat. We construct AI-IV-PoQ from an auxiliary-input version of commitments in a similar way, showing that (1)If auxiliary-input one-way functions exist (which exist if CZK⊈BPP), then AI-IV-PoQ exist. (2)If auxiliary-input collision-resistant hash functions exist (which is equivalent to PWPP⊈FBPP) or SZK⊈BPP, then constant-round AI-IV-PoQ exist.},
keywords = {Tuesday},
pubstate = {published},
tppubtype = {Talk}
}
Marco Aldi, Sevag Gharibian, Dorian Rudolph
Quantum complexity theory meets TFNP: Product Quantum Satisfiability on qudits Talk
2024.
@Talk{T24_50,
title = {Quantum complexity theory meets TFNP: Product Quantum Satisfiability on qudits},
author = {Marco Aldi and Sevag Gharibian and Dorian Rudolph},
year = {2024},
date = {2024-01-01},
abstract = {The theory of Total Function NP (TFNP) and its subclasses says that, even if one is promised an efficiently verifiable proof exists for a problem, finding this proof can be intractable. Despite being a classical complexity class, however, TFNP has made a surprise appearance in the study of Quantum Satisfiability (QSAT): If a QSAT instance has a System of Distinct Representatives (SDR), then it has a product-state solution [Laumann, Läuchli, Moessner, Scardicchio, and Sondhi 2010]. Efficiently finding this product-state solution, however, has remained elusive. In this work, we introduce a new framework based on Weighted SDRs (WSDR), which among other results, allows us to: (1) significantly simplify and extend the results of [LLMSS 2010] to qudit systems, (2) establish a connection to the Bézout number for multihomogeneous polynomial systems, and (3) apply the parameterized algorithm of [Aldi, de Beaudrap, Gharibian, Saeedi 2021] to solve new instances of QSAT efficiently on qudits. The second of these, in particular, allows us to define the first ""quantum-inspired"" subclass of TFNP, for which we show QSAT with SDR is complete. Thus, we obtain the first evidence that QSAT with SDR is, in fact, intractable.},
keywords = {Tuesday},
pubstate = {published},
tppubtype = {Talk}
}
Jiachen Hu, Tongyang Li, Xinzhao Wang, Yecheng Xue, Chenyi Zhang, Han Zhong
Quantum Non-Identical Mean Estimation: Efficient Algorithms and Fundamental Limits Talk
2024.
Abstract | Tags: Proceedings, Tuesday | Links:
@Talk{T24_281,
title = {Quantum Non-Identical Mean Estimation: Efficient Algorithms and Fundamental Limits},
author = {Jiachen Hu and Tongyang Li and Xinzhao Wang and Yecheng Xue and Chenyi Zhang and Han Zhong},
url = {https://arxiv.org/abs/2405.12838},
year = {2024},
date = {2024-01-01},
abstract = {We systematically investigate quantum algorithms and lower bounds for mean estimation given query access to non-identically distributed samples. On the one hand, we give quantum mean estimators with quadratic quantum speed-up given samples from different bounded or sub-Gaussian random variables. On the other hand, we prove that, in general, it is impossible for any quantum algorithm to achieve quadratic speed-up over the number of classical samples needed to estimate the mean μ, where the samples come from different random variables with mean close to μ. Technically, our quantum algorithms reduce bounded and sub-Gaussian random variables to the Bernoulli case, and use an uncomputation trick to overcome the challenge that direct amplitude estimation does not work with non-identical query access. Our quantum query lower bounds are established by simulating non-identical oracles by parallel oracles, and also by an adversarial method with non-identical oracles. Both results pave the way for proving quantum query lower bounds with non-identical oracles in general, which may be of independent interest.},
keywords = {Proceedings, Tuesday},
pubstate = {published},
tppubtype = {Talk}
}
Shubham P. Jain, Joseph T. Iosue, Alexander Barg, Victor V. Albert
Quantum Spherical Codes Talk
2024.
Abstract | Tags: Tuesday | Links:
@Talk{T24_354,
title = {Quantum Spherical Codes},
author = {Shubham P. Jain and Joseph T. Iosue and Alexander Barg and Victor V. Albert},
url = {https://arxiv.org/abs/2302.11593},
year = {2024},
date = {2024-01-01},
abstract = {I'll introduce a framework for constructing quantum codes defined on spheres, taking inspiration from classical spherical codes. The framework is applied to bosonic coding, obtaining multimode extensions of the cat codes that can outperform previous constructions while requiring a similar type of overhead. Our polytope-based cat codes consist of sets of points with large separation that at the same time form averaging sets known as spherical designs, a property sufficient to guarantee protection against photon losses.},
keywords = {Tuesday},
pubstate = {published},
tppubtype = {Talk}
}
Bo Yang, Elham Kashefi, Dominik Leichtle, Harold Ollivier
State Purification with Symmetry Subgroup Projectors Talk
2024.
@Talk{T24_464,
title = {State Purification with Symmetry Subgroup Projectors},
author = {Bo Yang and Elham Kashefi and Dominik Leichtle and Harold Ollivier},
year = {2024},
date = {2024-01-01},
abstract = {Quantum state purification is the functionality that, given multiple copies of an unknown state, outputs a state with increased purity. This is an essential building block for the near- and middle-term quantum ecosystems before the availability of full fault tolerance, where one may want to obtain purified quantum states instead of expectation values. We propose an effective state purification gadget with a moderate quantum overhead by projecting multiple noisy quantum inputs to their symmetry subspace defined by a set of projectors forming a subgroup of the symmetry group. This provides a state purification performance scaling inverse-linearly to the number of state copies given a fixed stochastic error rate, which drastically improves the implementation overhead in previous works. Our method may find its application in designing robust verification protocols for quantum outputs before the availability of fully fault-tolerant computing.},
keywords = {Tuesday},
pubstate = {published},
tppubtype = {Talk}
}
André Chailloux, Jean-Pierre Tillich
The Quantum Decoding Problem Talk
2024.
Abstract | Tags: Proceedings, Tuesday
@Talk{T24_222,
title = {The Quantum Decoding Problem},
author = {André Chailloux and Jean-Pierre Tillich},
year = {2024},
date = {2024-01-01},
abstract = {One of the founding results of lattice based cryptography is a quantum reduction from the Short Integer Solution (SIS) problem to the Learning with Errors (LWE) problem introduced by Regev. It has recently been pointed out by Chen, Liu and Zhandry[CLZ22] that this reduction can be made more powerful by replacing the LWE problem with a quantum equivalent, where the errors are given in quantum superposition. In parallel, Regev's reduction has recently been adapted in the context of code-based cryptography by Debris, Remaud and Tillich[DRT23], who showed a reduction between the Short Codeword Problem and the Decoding Problem (the DRT reduction). This motivates the study of the Quantum Decoding Problem (QDP), which is the Decoding Problem but with errors in quantum superposition and see how it behaves in the DRT reduction. The purpose of this paper is to introduce and to lay a firm foundation for QDP. We first show QD Pis likely to be easier than classical decoding, by proving that it can be solved in quantum polynomial time in a large regime of noise whereas no non-exponential quantum algorithm is known for the classical decoding problem. Then, we show that QDP can even be solved (albeit not necessarily efficiently) beyond the information theoretic Shannon limit for classical decoding. We give precisely the largest noise level where we can solve QDP giving in a sense the information theoretic limit for this new problem. Finally, we study how QDP can be used in the DRT reduction. First, we show that our algorithms can be properly used in the DRT reduction showing that our quantum algorithms for QDP beyond Shannon capacity can be used to find minimal weight codewords in a random code. On the negative side, we show that the DRT reduction cannot be, in all generality, a reduction between finding small codewords and QDP by exhibiting quantum algorithms for QDP where this reduction entirely fails. Our proof techniques include the use of specific quantum measurements, such as q-ary unambiguous state discrimination and pretty good measurements as well as strong concentration bounds on weight distribution of random shifted dual codes, which we relate using quantum Fourier analysis.},
keywords = {Proceedings, Tuesday},
pubstate = {published},
tppubtype = {Talk}
}
Yixian Qiu, Kelvin Koor, Patrick Rebentrost
The Quantum Esscher Transform Talk
2024.
Abstract | Tags: Tuesday | Links:
@Talk{T24_431,
title = {The Quantum Esscher Transform},
author = {Yixian Qiu and Kelvin Koor and Patrick Rebentrost},
url = {https://arxiv.org/pdf/2401.07561},
year = {2024},
date = {2024-01-01},
abstract = {The Esscher Transform is a tool of broad utility in various domains of applied probability. It provides the solution to a constrained minimum relative entropy optimization problem. In this work, we study the generalization of the Esscher Transform to the quantum setting. We examine a relative entropy minimization problem for a quantum density operator, potentially of wide relevance in quantum information theory. The resulting solution form motivates us to define the textitquantum Esscher Transform, which subsumes the classical Esscher Transform as a special case. Envisioning potential applications of the quantum Esscher Transform, we also discuss its implementation on fault-tolerant quantum computers. Our algorithm is based on the modern techniques of block-encoding and quantum singular value transformation (QSVT). We show that given block-encoded inputs, our algorithm outputs a subnormalized block-encoding of the quantum Esscher transform within accuracy ε in $tilde O(kappa d łog^2 1/epsilon)$ queries to the inputs, where κ is the condition number of the input density operator and d is the number of constraints.},
keywords = {Tuesday},
pubstate = {published},
tppubtype = {Talk}
}
Junqiao Lin
Tracial embeddable strategies: Lifting MIP* tricks to MIPco Talk
2024.
Abstract | Tags: Tuesday | Links:
@Talk{T24_130,
title = {Tracial embeddable strategies: Lifting MIP* tricks to MIPco},
author = {Junqiao Lin},
url = {https://arxiv.org/abs/2304.01940},
year = {2024},
date = {2024-01-01},
abstract = {We prove that any two-party correlation in the commuting operator model can be approximated using a tracial embeddable strategy, a class of strategy defined on a finite tracial von Neumann algebra, which we define in this paper. Using this characterization, we show that any approximately synchronous correlation can be approximated to the average of a collection of synchronous correlations in the commuting operator model. This generalizes the result from Vidick [JMP 2022], which only applies to finite-dimensional quantum correlations. Furthermore, we extend the state-dependent norm variant of the Gowers-Hatami theorem to finite von Neumann algebras. Combined with the aforementioned characterization, this enables us to lift many known results about robust self-testing for non-local games to the commuting operator model, including a sample efficient EPR testing for the commuting operator strategies. We believe that, in addition to the contribution from this paper, this class of strategies can be helpful for further understanding non-local games in the infinite-dimensional setting.},
keywords = {Tuesday},
pubstate = {published},
tppubtype = {Talk}
}
Kieran Mastel, William Slofstra
Two prover perfect zero knowledge for MIP* Talk
2024.
Abstract | Tags: Tuesday | Links:
@Talk{T24_139,
title = {Two prover perfect zero knowledge for MIP*},
author = {Kieran Mastel and William Slofstra},
url = {https://doi.org/10.48550/arXiv.2404.00926},
year = {2024},
date = {2024-01-01},
abstract = {The recent MIP*=RE theorem of Ji, Natarajan, Vidick, Wright, and Yuen shows that the complexity class MIP* of multiprover proof systems with entangled provers contains all recursively enumerable languages. Prior work of Grilo, Slofstra, and Yuen [FOCS '19] further shows (via a technique called simulatable codes) that every language in MIP* has a perfect zero knowledge (PZK) MIP* protocol. The MIP*=RE theorem uses two-prover one-round proof systems, and hence such systems are complete for MIP*. However, the construction in Grilo, Slofstra, and Yuen uses six provers, and there is no obvious way to get perfect zero knowledge with two provers via simulatable codes. This leads to a natural question: are there two-prover PZK-MIP* protocols for all of MIP*? In this paper, we show that every language in MIP* has a two-prover one-round PZK-MIP* protocol, answering the question in the affirmative. For the proof, we use a new method based on a key consequence of the MIP*=RE theorem, which is that every MIP* protocol can be turned into a family of boolean constraint system (BCS) nonlocal games. This makes it possible to work with MIP* protocols as boolean constraint systems, and in particular allows us to use a variant of a construction due to Dwork, Feige, Kilian, Naor, and Safra [Crypto '92] which gives a classical MIP protocol for 3SAT with perfect zero knowledge. To show quantum soundness of this classical construction, we develop a toolkit for analyzing quantum soundness of reductions between BCS games, which we expect to be useful more broadly. This toolkit also applies to commuting operator strategies, and our argument shows that every language with a commuting operator BCS protocol has a two prover PZK commuting operator protocol.},
keywords = {Tuesday},
pubstate = {published},
tppubtype = {Talk}
}
Zhenhuan Liu, Xingjian Zhang, Yue-Yang Fei, Zhenyu Cai
Virtual Channel Purification Talk
2024.
Abstract | Tags: Tuesday | Links:
@Talk{T24_316,
title = {Virtual Channel Purification},
author = {Zhenhuan Liu and Xingjian Zhang and Yue-Yang Fei and Zhenyu Cai},
url = {https://arxiv.org/abs/2402.07866},
year = {2024},
date = {2024-01-01},
abstract = {Quantum error mitigation is a key approach for extracting target state properties on state-of-the-art noisy machines and early fault-tolerant devices. Using the ideas from flag fault tolerance and virtual state purification, we develop the virtual channel purification (VCP) protocol, which consumes similar qubit and gate resources as virtual state purification but offers up to exponentially stronger error suppression with increased system size and more noisy operation copies. Furthermore, VCP removes most of the assumptions required in virtual state purification. Essentially, VCP is the first quantum error mitigation protocol that does not require specific knowledge about the noise models, the target quantum state, and the target problem while still offering rigorous performance guarantees for practical noise regimes. Further connections are made between VCP and quantum error correction to produce one of the first protocols that combine quantum error correction and quantum error mitigation beyond concatenation. We can remove all noise in the channel while paying only the same sampling cost as low-order purification, reaching beyond the standard bias-variance trade-off in quantum error mitigation. Our protocol can also be adapted to key tasks in quantum networks like channel capacity activation and entanglement distribution.},
keywords = {Tuesday},
pubstate = {published},
tppubtype = {Talk}
}